Temporal hypergraphs provide a powerful paradigm for modeling time-dependent, higher-order interactions in complex systems. Representation learning for hypergraphs is essential for extracting patterns of the higher-order interactions that are critically important in real-world problems in social network analysis, neuroscience, finance, etc. However, existing methods are typically designed only for specific tasks or static hypergraphs. We present CAT-Walk, an inductive method that learns the underlying dynamic laws that govern the temporal and structural processes underlying a temporal hypergraph. CAT-Walk introduces a temporal, higher-order walk on hypergraphs, SetWalk, that extracts higher-order causal patterns. CAT-Walk uses a novel adaptive and permutation invariant pooling strategy, SetMixer, along with a set-based anonymization process that hides the identity of hyperedges. Finally, we present a simple yet effective neural network model to encode hyperedges. Our evaluation on 10 hypergraph benchmark datasets shows that CAT-Walk attains outstanding performance on temporal hyperedge prediction benchmarks in both inductive and transductive settings. It also shows competitive performance with state-of-the-art methods for node classification.

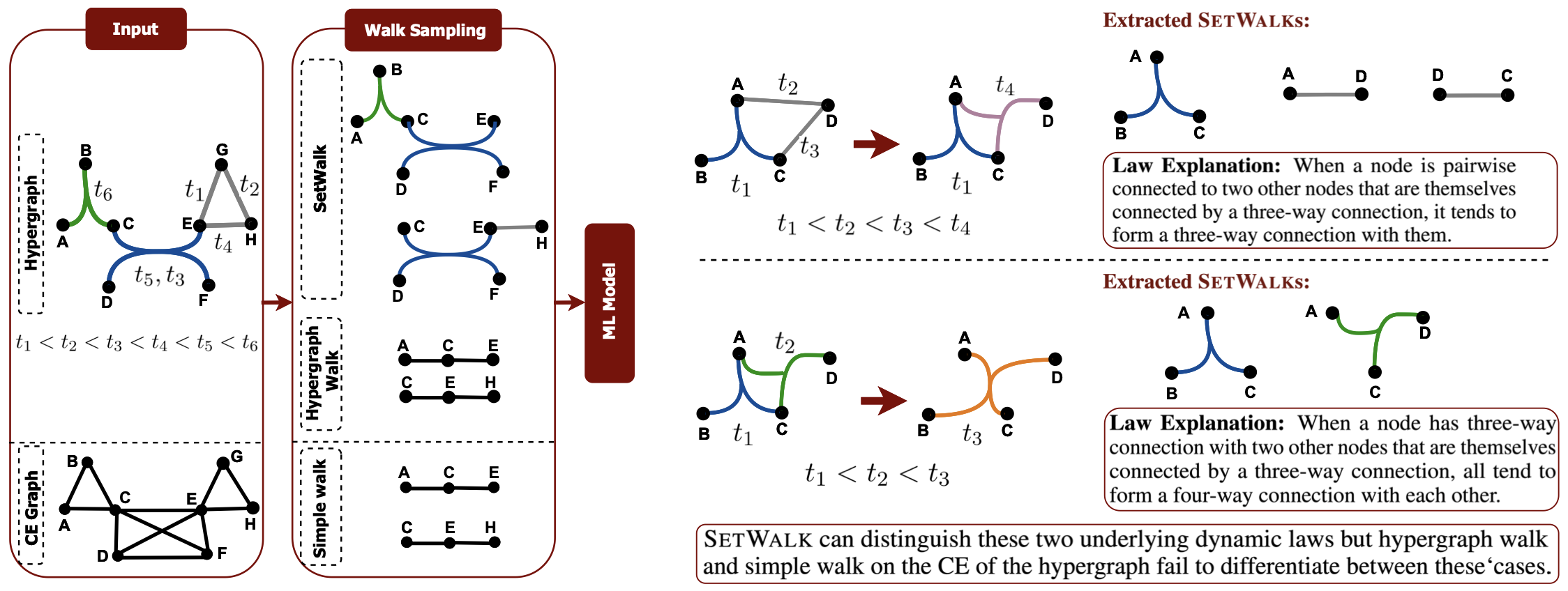
Capturing underlying temporal and higher-order structure

Many recent attempts to design representation learning methods for hypergraphs are equivalent to applying Graph Neural Networks (GNNs) to the clique-expansion (CE) of a hypergraph. CE is a straightforward way to generalize graph algorithms to hypergraphs by replacing hyperedges with (weighted) cliques. However, we prove that this decomposition of hyperedges limits expressiveness, leading to suboptimal performance. New methods that encode hypergraphs directly partially address this issue but these methods suffer from some combination of the following three limitations: they are designed for (1) learning the structural properties of static hypergraphs and do not consider temporal properties, (2) the transductive setting, limiting their performance on unseen patterns and data, and (3) a specific downstream task (e.g., node classification, hyperedge prediction, or subgraph classification) and cannot easily be extended to other downstream tasks, limiting their application. To address these challenges, we propose a higher-order temporal walk, called SetWalk, to capture both higher-order and temporal properties, and then design a provably powerful permutation invariant pooling method to learn the hyperedge representations.

SetWalks

One possible solution to capturing underlying temporal and higher-order structure is to extend the concept of a hypergraph random walk to its temporal counterpart by letting the walker walk over time. However, existing definitions of random walks on hypergraphs offer limited expressivity and sometimes degenerate to simple walks on the CE of the hypergraph. There are two reasons for this: (1) Random walks are composed of a sequence of pair-wise interconnected vertices, even though edges in a hypergraph connect sets of vertices. Decomposing them into sequences of simple pair-wise interactions loses the semantic meaning of the hyperedges. (2) A sampling probability of a walk on a hypergraph must be different from its sampling probability on the CE of the hypergraph. To this end, we present a new temporal higher-order walks, called SetWalk, where each random walk is a sequence of hyperedges (i.e., in each step of walk sampling, we sample an adjacent hyperedge).

SetMixer

Hyperedge Prediction:

Node Classification:

MLP-Mixer vs RNNs: